理学科 数学コース
学科公式サイト
詳しい情報につきましては、理学科 数学コースサイトでご案内しています。
学科・コース紹介
数学 ー時代にとらわれない普遍的な学問ー
古代ギリシャに端を発し、現代も発展を続ける数学。代数学・幾何学・解析学という純粋数学は、あらゆる科学技術の基礎として、またグラフ理論や暗号理論などの数学は、ネットワークが高度に発達した社会において、その実用的な運用や発展のために不可欠な存在です。当コースは、数学を専門に学べる高等教育機関として理工学部開設当時から60年もの歴史と実績を有しています。各方面にわたる数学研究の第一線で活躍しているスタッフが、最新の研究成果に基づく充実した教育を提供します。
数学に夢をもち、自らの力を信じて挑戦する人間の育成。
当コースでは、数学を通して論理的思考力や総合的判断力、問題解決能力を身につけ、人生を自ら切り開くことのできる学生を育てます。そのため、コースの教員から直接指導を受けられる少人数制のゼミや対話形式の講義、プレゼンテーションの機会を豊富に用意しています。こうして、従来の一方向の講義では困難な、学生の理解度に合わせた指導を実現します。3年次の「数学講究」(教員志望クラス)では、3年次が1年次の演習を補佐することで、教育実習を想定した実践経験を積む機会も提供します。
カリキュラム
純粋数学から応用数学まで、対話型講義で学びます。
数学コースでは、代数学・幾何学・解析学などの純粋数学を体系的に学んだ後、グラフ理論や暗号理論など、応用数学を学習します。理論を一方的に教えるのではなく、知的好奇心をベースに、個別対話型で学ぶスタイルを重視するなど、創造性や柔軟性を伸ばす工夫を取り入れています。
学びのSTEP
| 専門科目 | 1年次 | 2年次 | 3年次 | 4年次 |
|---|---|---|---|---|
| 必修科目 | 数学講究(1)[2] 数学講究(2)[2] 線形数学(1)[4] 基礎解析学(1)[4] |
数学講究(3)[2] 数学講究(4)[2] 数学講究(5)[2] 数学講究(6)[2] |
数学講究(7)[2] 数学講究(8)[2] |
卒業研究[8] |
| 選択必修科目 | 現代数学(1)[2] 現代数学(2)[2] 現代数学(3)[2] 現代数学(4)[2] 現代数学(5)[2] 応用数学(1)[2] 応用数学(2)[2] |
|||
| 選択科目 | 基礎幾何学[2] | 線形数学(2)[2] 基礎解析学(2)[2] 群論(1)[2] 群論(2)[2] 集合と位相(1)[2] 集合と位相(2)[2] 微分方程式論(1)[2] 微分方程式論(2)[2] 計算機実習(1)[2] 複素解析学(1)[2] 教科教育演習[1] 地学概論I[2] 地学概論II[2] 地学実験[1] データ構造とアルゴリズムI[2] オペレーティングシステム[2] |
複素解析学(2)[4] 代数学(1)[4] 代数学(2)[4] 幾何学(1)[4] 幾何学(2)[4] 実解析学(1)[4] 実解析学(2)[4] 数理統計学(1)[2] 数理統計学(2)[2] 計算機実習(2)[1] 実験数理解析[1] 情報理論[2] 通信方式[2] データベース論I[2] 画像処理[2] ネットワーク工学[2] コンピュータグラフィックス[2] 組み込みシステム概論[2] 移動体通信工学[2] 情報と社会[2] |
情報と職業[2] |
- [ ]内の数字は単位数
Pick up授業
数学講究(1)
補足講義を受けながら、微分積分学と線形代数学の演習問題に取り組みます。計算や証明の基本的な技術を身につけ理論の理解を深めるとともに、別解の可能性や問題解決の方法について教員や学生同士で議論しながら数学的なセンスを磨いていきます。

群論(1)
群とは演算を一つだけもつ代数系です。足し算のみに注目した場合の整数全体や、図形の対称移動(移動や裏返しでもとの図形と重ね合わせられるような操作)も群をなしますが、他の数学的対象へ作用させることで、それらの性質がよく分かることもあります。群論を極めるとルービックキューブの解析も可能です。
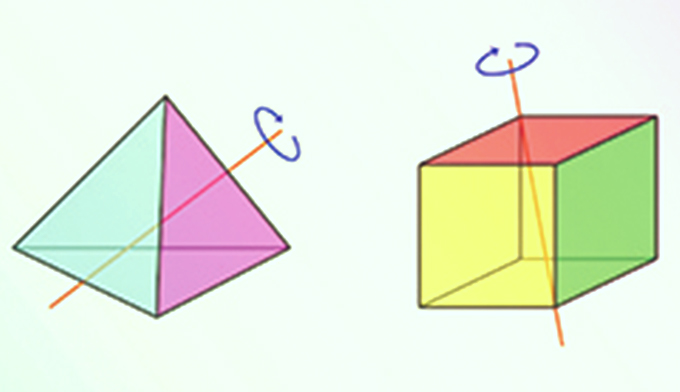
応用数学(1)
離散数学の一分野であるグラフ理論について取り扱います。グラフ理論におけるグラフとは、点の集合とそれらの点を結ぶ線の集合からなるもので、分子構造や道路網や人間関係などを抽象化したものです。そのため、グラフ理論は数学の分野にとどまらず自然科学や社会科学などの分野にも幅広く応用できます。
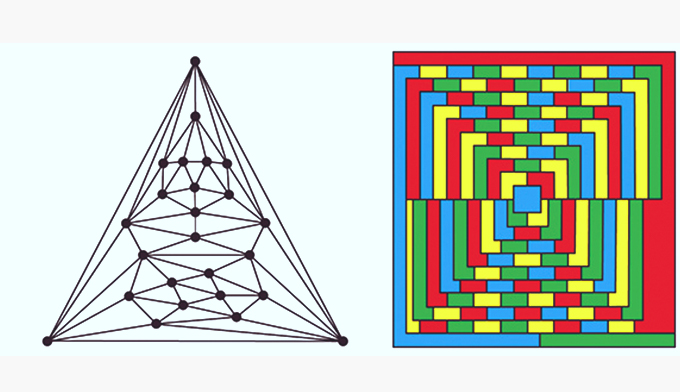
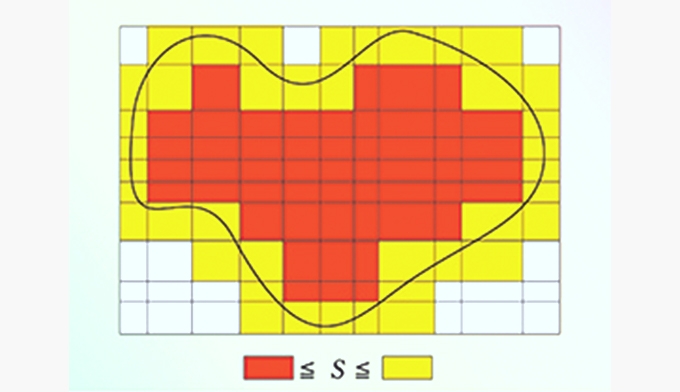
実解析学(1)
面積とは何か、いかに測るべきか、というのは、人類が数学と出合ったときからの問題です。私たちは小学校での図形の面積公式から高校や大学初年級の積分まで、面積に関する種々の数学を学びますが、厳密な数学理論のためには不十分です。本科目では面積の一般化といえる「測度」について学びます。これは実解析学(2)の「ルベーグ積分」の理論の基礎となります。
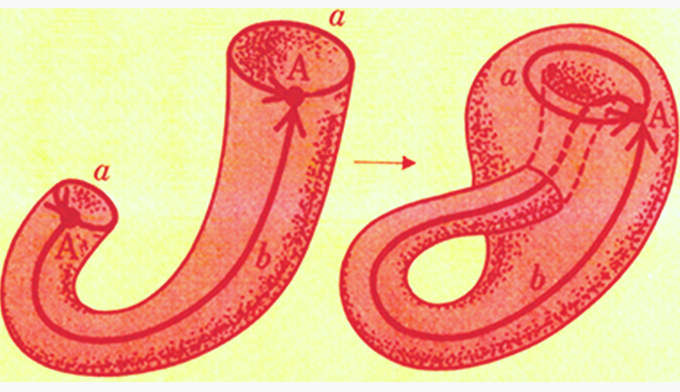
幾何学(2)
位相空間に複体の構造を定め、その複体のホモロジー群やオイラー標数などの位相不変量を計算します。図は「クラインの壺」の絵ですが、そのホモロジー群の計算のために完全系列という代数的手段を導入し、クラインの壺を含めさまざまな閉曲面のホモロジーを計算し、同相分類を行います。
数学講究(7)
セミナー形式で専門書の輪読を行い、卒業研究を念頭に自ら数学を学ぶ力を養います。教員志望クラスでは、1年生の演習問題を題材に、数学の解説だけでなく、数学を教えることや授業の仕方についても学び、1年生の演習補助や黒板による問題解説を実際に行うことで授業体験をします。

カリキュラムの特色
- 現代数学の基礎・基本を習得・復習する、多角的な学び
- 教育実習を想定し、3年生が1年生の演習を補助する講義
- 世界最先端の数学研究について扱う、専門的な講義
3つのポイント
1.数学の教員を目指す人を、強力にサポート。
教員になりたい学生をサポートするために、3年生が1年生を指導する専門カリキュラムを設けています。

2.大阪府内でも数少ない、数学に特化した私大教育。
数多い大阪府内の私大の中でも数少ない、数学を専門的に学べる学科です。充実した教員に加え、さまざまなカリキュラムにより、基礎から応用まで幅広い知識を習得できます。

3.楽しいイベントでレベルアップを図る。
学内・学外を問わずに誰でも参加できる「数学コンテスト」を毎年実施しています。脳を活性化し、数学の知識を楽しく学ぶことが可能です。

進路
教員を選ぶ人が多数。民間企業でも多彩な分野で活躍できます。
理学科数学コースの特徴の一つに、教員をめざす人や大学院への進学をめざす人の多いことが挙げられます。実際、数学コースの学生の半数以上が、教員、教育関連企業や大学院への進学を果たしています。また、情報通信業や金融・保険業をはじめ、さまざまな分野で多くの卒業生たちが活躍しています。
卒業生の主な進路
| 主な就職・進学先 | |
|---|---|
| 民間企業 | 東芝/パーソルビジネスプロセスデザイン/りそな銀行/関西みらい銀行/池田泉州銀行/日立ソリューションクリエイト/NXキャッシュ・ロジスティクスNTTデータMSE/三菱総研DCS |
| 公務員・教員 | 和歌山県庁/滋賀県庁/長浜市役所/堺市役所/大阪府教育委員会/東大阪市教育委員会/奈良県教育委員会/和歌山県教育委員会/尼崎市教育委員会/堺市教育委員会/和歌山大学/大阪産業大学/大阪学院大学/浪速高等学校・中学校/関西金光学園/追手門学院/清明学院高等学校/明徳学園/明浄学院 |
| 大学院進学 | 近畿大学大学院/神戸大学大学院/熊本大学大学院/大阪教育大学大学院 |
※令和5年度(2023年度)、令和6年度(2024年度)卒業生実績
業種別進路先
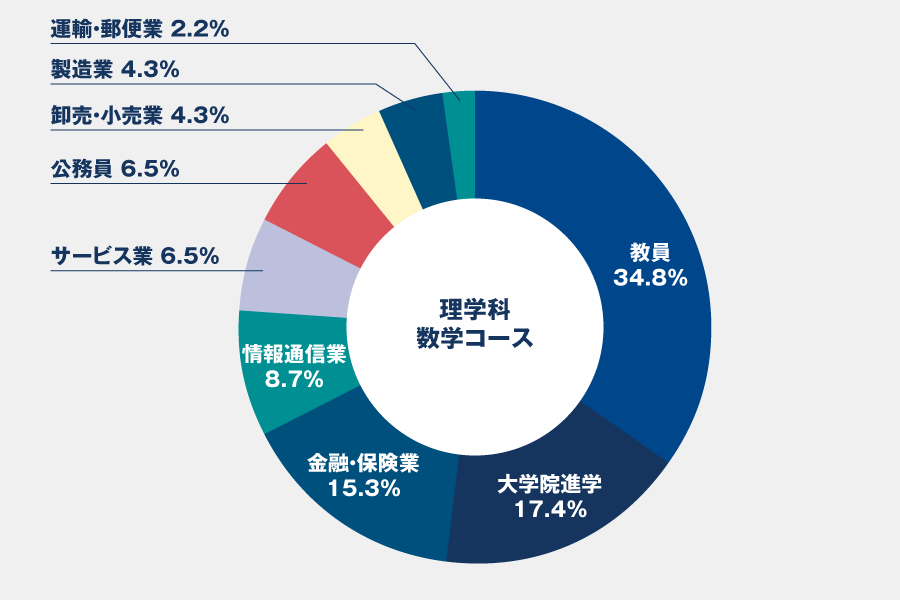
※2024年度卒実績
※割合の合計は、端数処理の関係で100%にならないことがあります
資格
所定の単位修得で取得できる資格
高等学校教諭一種免許状(数学/理科/情報)/中学校教諭一種免許状(数学/理科)/図書館司書
理工学部共通
ITパスポート/基本情報技術者
