Academic Staff and Fellows

- In Dae JONG
- Associate Professor Doctor of Science
- Department/Science Graduate school/Science
Research is conducted into knot theory and low-dimension topology (3D and 4D). To investigate knots mathematically, often the invariants of knots are used. Research takes an interest in the relation between the algebraic properties of invariants and the geometrical properties of knots.
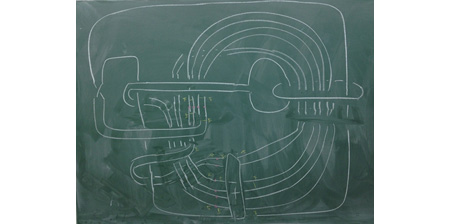
A knot used in a study on Dehn surgery
| Research Area | Knot Theory |
|---|---|
| Research Interests | Study on knots and 3-manifold via Dehn surgery Relationship between a geometric property of a knot and an algebraic property of its invariant |
| Selected Publications |
(1) Infinitely many knots admitting the same integer surgery and a 4-dimensional extension, T. Abe, I. D. Jong, J. Luecke, J. Osoinach, Int. Math. Res. Notices, 22 (2015), 11667--11693. (2) Cyclic and finite surgeries on Montesinos knots, K. Ichihara, I. D. Jong, Algebr. Geom. Topol. 9 (2009), no. 2, 731--742. (3) Alexander polynomials of alternating knots of genus two, I. D. Jong, Osaka J. Math. 46 (2009), no. 2, 353--371. |
| Affiliated Academic Societies | The Mathematical Society of Japan |
| Education (Undergraduate Course) |
Ritsumeikan University |
| Education (Master's/Doctral Course) |
Osaka City University |
| Title of Thesis, Institute, Date | Alexander polynomials of alternating knots,Osaka City University,2010/3 |
Knot Theory Laboratory
jong(at)math.kindai.ac.jp
|