Academic Staff and Fellows

IKEDA Toru: Professor Doctor of Mathematical Sciences; Department/Science　 Graduate school/Science

A 3-manifold is a space in which a 3D coordinate system can be drawn around arbitrary points. Although it’s difficult to visualize an entire 3-manifold, work here involves cutting and pasting spaces and curves in order to study geometric properties such as symmetry.

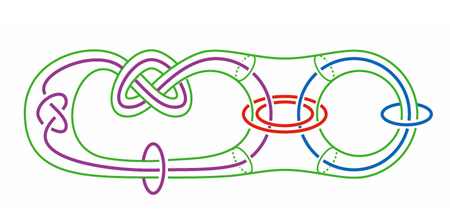
Symmetric link exterior

Research Area	Topology, 3D Manifolds, Knot Theory
Research Interests	Finite Group Actions on 3-Manifolds Symmetries of Knots and Spatial Graphs
Selected Publications	(1) Realization of graph symmetries through spatial embeddings into the 3-sphere, Topol. Appl. 282 (2020), 107313. (2) Cyclically symmetric hyperbolic spatial graphs in 3-manifolds, Geom. Dedicata 170 (2014), 177--183. (3) Finite group actions on homologically peripheral 3-manifolds, Math. Proc. Cambridge Philos. Soc. 151 (2011), 319--337.
Research and Achievements	01_ikeda_toru.pdf
Education (Undergraduate Course)	BE from University of Tokyo
Education (Master's/Doctral Course)	ME and DE from University of Tokyo

Manifold Laboratory

E-mail	ikeda（at）math.kindai.ac.jp Note that this e-mail address has replaced the "@" with "(at)" to prevent spam. When e-mailing, replace the "(at)" with "@".