Academic Staff and Fellows

In Dae JONG: Associate Professor Doctor of Science; Department/Science　 Graduate school/Science

Research is conducted into knot theory and low-dimension topology (3D and 4D). To investigate knots mathematically, often the invariants of knots are used. Research takes an interest in the relation between the algebraic properties of invariants and the geometrical properties of knots.

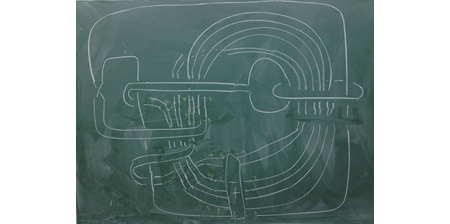
A knot used in a study on Dehn surgery

Research Area	Knot Theory
Research Interests	Study on knots and 3-manifold via Dehn surgery Relationship between a geometric property of a knot and an algebraic property of its invariant
Selected Publications	(1) Infinitely many knots admitting the same integer surgery and a 4-dimensional extension, T. Abe, I. D. Jong, J. Luecke, J. Osoinach, Int. Math. Res. Notices, 22 (2015), 11667--11693. (2) Cyclic and finite surgeries on Montesinos knots, K. Ichihara, I. D. Jong, Algebr. Geom. Topol. 9 (2009), no. 2, 731--742. (3) Alexander polynomials of alternating knots of genus two, I. D. Jong, Osaka J. Math. 46 (2009), no. 2, 353--371.
Affiliated Academic Societies	The Mathematical Society of Japan
Education (Undergraduate Course)	Ritsumeikan University
Education (Master's/Doctral Course)	Osaka City University
Title of Thesis, Institute, Date	Alexander polynomials of alternating knots，Osaka City University，2010/3

Knot Theory Laboratory

E-mail	jong（at）math.kindai.ac.jp Note that this e-mail address has replaced the "@" with "(at)" to prevent spam. When e-mailing, replace the "(at)" with "@".