教員・研究員紹介
- 山下 登茂紀 （やました ともき）
- 教授 博士（理学）
- 所属学科/理学科 数学コース 所属専攻/理学専攻
- 研究キーワード：
- ベクトル・行列／線形代数／組合せ／離散数学、グラフ理論／数理統計、数理モデル／応用数学
離散的な構造の多くはグラフとして記述でき、それらを扱うグラフ理論は離散数学の大きな研究分野の一つです。なかでも極値グラフ理論と呼ばれるグラフの部分構造と不変量の関係を研究しています。
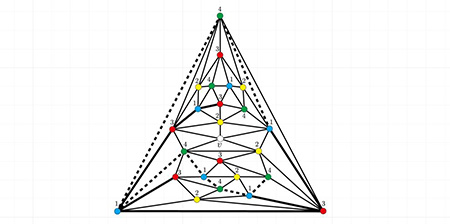
Heawood's counterexample to Kempe's "proof"
| 専門 | グラフ理論 |
|---|---|
| 担当科目（学部） | 近大ゼミ1、数学講究(1)、数学講究(2)、数学講究(3)、数学講究(8)、科学技術英語2、応用数学(2) |
| 担当科目（大学院） | 離散数理特論、組合せ数学特論、数理解析特別研究 |
| 主な研究テーマ | グラフにおいて，特別な性質を持った閉路や木が存在するための次数条件 |
| 代表的な研究業績 |
(1) Minimum degree conditions for the existence of a sequence of cycles whose lengths differ by one or two, S.Chiba, K.Ota and T.Yamashita, Journal of Graph Theory 103 (2023) 340--358. (2) A degree sum condition on the order, the connectivity and the independence number for Hamiltonicity, S.Chiba, M.Furuya, K.Ozeki, M.Tsugaki and T.Yamashita, Electronic Journal of Combinatorics~26 (4) P4.53 (2019). (3) Degree Conditions for the Existence of Vertex-Disjoint Cycles and Paths: A Survey, S.Chiba and T.Yamashita, Graphs Combin. 34 (2018) 1--83. |
| 研究内容・研究成果 | |
| researchmap | http://researchmap.jp/YamashitaTomoki |
| 所属学協会 | 日本数学会 |
| 出身大学 | 神戸大学 |
| 出身大学院 | 神戸大学大学院 |
| 論文名、取得大学、取得年月 | Dominating cycles in graphs、神戸大学、２００４年３月 |
| 主な経歴 | 2004年 慶應義塾大学 理工学部 特別研究助手 2005年 朝日大学 歯学部 講師 2008年 北里大学 一般教育部 講師 2011年 近畿大学 理工学部 講師 2015年 近畿大学 理工学部 准教授 2022年 近畿大学 理工学部 教授 |
| 学生へのアドバイス | 数学に限らず何事も、頑張るのではなく、楽しんで挑戦していけば意外とうまくいったりすることもあります。学生生活、頑張ろうと思わずに楽しもうと思って過ごしてください。 |
| 学生に薦めたい書物 | 数学ビギナーズマニュアル 佐藤文広 日本評論社 |
離散数学研究室
| 教員室 | ３１号館３階山下教授室 |
|---|---|
| メールアドレス | yamashita（at）math.kindai.ac.jp
|
| 研究室URL |
https://www.math.kindai.ac.jp/laboratory/yamashita/ |