教員・研究員紹介
-
鈴木 貴雄
(すずき たかお)
- 准教授 博士(理学)
-
所属学科/理学科 数学コース
所属専攻/理学専攻
- 研究キーワード:
- 方程式/ベクトル・行列/線形代数/数学、解析学/関数/微分積分/複素数/組合せ
複素領域上の微分・差分方程式、およびその解として定義される特殊関数について研究しています。特殊関数は純粋数学及び応用数学の様々な分野と繫がりのある、とても魅力的な研究対象です。
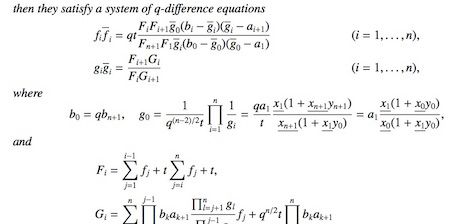
A型離散パンルヴェ系
| 専門 |
特殊関数、可積分系 |
| 担当科目(学部) |
微分積分学I、近大ゼミ2、数学講究(2)、数学講究(4)、微分方程式論(2)、実解析学(1) |
| 担当科目(大学院) |
特殊関数特論、関数方程式特論、数理解析特別研究、特殊関数特別研究、数理解析演習 |
| 主な研究テーマ |
パンルヴェ方程式の研究
超幾何関数の研究
無限次元可積分系の研究 |
| 代表的な研究業績 |
(1) Generalized q-Painlevé system of type (A2n+1+A1+A1)(1) arising from cluster algebra, Naoto Okubo and Takao Suzuki, Int. Math. Res. Not. 2022(9) 6561-6607 (2022).
(2) An affine Weyl group action on the basic hypergeometric series arising from the q-Garnier system, Taiki Idomoto and Takao Suzuki, Lett. Math.Phys. 112(6) (2022).
(3) A continuous limit of the q-Garnier system, Kazuya Matsugashita and Takao Suzuki, RIMS Kokyuroku Bessatsu B96 101-116 (2024).
|
| researchmap |
http://researchmap.jp/suzukit |
| 所属学協会 |
日本数学会 |
| 学外活動 |
日本数学会 地方区・全国区代議員(2019年3月〜2022年2月) |
| 出身大学 |
神戸大学 |
| 出身大学院 |
神戸大学 |
| 論文名、取得大学、取得年月 |
Affine Weyl group symmetry of the Garnier system、神戸大学、2004年3月 |
| 主な経歴 |
2011年 大阪府立大学教育拠点形成教員
2012年 近畿大学講師
2016年 近畿大学准教授 |
| 受賞歴 |
全学共通教育ベストティーチャー賞(神戸大学、2010年10月) |
| 学生へのアドバイス |
大学を卒業して社会に出た後でも勉強は常に必要となります。大学では単に知識を覚えるのではなく、新しい知識を身に付ける能力を養って下さい。 |
特殊関数研究室
教員・研究員紹介
array(87) {
["professor_id"]=>
string(3) "643"
["site"]=>
string(3) "sci"
["html"]=>
string(15) "01_suzuki_takao"
["login_id"]=>
string(24) "suzuki@math.kindai.ac.jp"
["login_pw"]=>
string(64) "327a5f928f22872e97e8acb666921a0718a14014c6c8600398f4ed9caaf58aab"
["name"]=>
string(13) "鈴木 貴雄"
["name_en"]=>
string(12) "SUZUKI Takao"
["name_kana"]=>
string(19) "すずき たかお"
["jobtype"]=>
string(1) "3"
["degree"]=>
string(18) "博士(理学)"
["degree_en"]=>
string(32) "Ph.D (Science) (Kobe University)"
["department"]=>
string(30) "department_science_mathematics"
["department_txt"]=>
string(0) ""
["department_txt_en"]=>
string(0) ""
["major1"]=>
string(23) "graduate_school_science"
["major2"]=>
string(0) ""
["category1"]=>
string(32) "research_mathematics_and_physics"
["class1"]=>
string(34) "research_mathematics_and_physics03"
["category2"]=>
string(0) ""
["class2"]=>
NULL
["category3"]=>
string(0) ""
["class3"]=>
NULL
["specialty"]=>
string(27) "特殊関数、可積分系"
["specialty_en"]=>
string(40) "Special functions and Integrable systems"
["subject"]=>
string(126) "微分積分学I、近大ゼミ2、数学講究(2)、数学講究(4)、微分方程式論(2)、実解析学(1)"
["subject_en"]=>
string(0) ""
["subject_graduate"]=>
string(117) "特殊関数特論、関数方程式特論、数理解析特別研究、特殊関数特別研究、数理解析演習"
["subject_graduate_en"]=>
string(0) ""
["research_theme"]=>
string(94) "パンルヴェ方程式の研究
超幾何関数の研究
無限次元可積分系の研究"
["research_theme_en"]=>
string(85) "Painleve equations
Hypergeometric functions
Infinite dimensional integrable systems"
["research_record"]=>
string(903) "(1) <em>Generalized q-Painlevé system of type (A<sub>2n+1</sub>+A<sub>1</sub>+A<sub>1</sub>)<sup>(1) </sup>arising from cluster algebra</em>, Naoto Okubo and Takao Suzuki, Int. Math. Res. Not. <strong>2022</strong>(9) 6561-6607 (2022).<br />
<br />
(2) <em>An affine Weyl group action on the basic hypergeometric series arising from the q-Garnier system,</em> Taiki Idomoto and Takao Suzuki, Lett. Math.Phys. <strong>112</strong>(6) (2022).<br />
<br />
(3) <em>A continuous limit of the q-Garnier system,</em> Kazuya Matsugashita and Takao Suzuki, RIMS Kokyuroku Bessatsu <strong>B96</strong> 101-116 (2024)."
["research_record_en"]=>
string(903) "(1) <em>Generalized q-Painlevé system of type (A<sub>2n+1</sub>+A<sub>1</sub>+A<sub>1</sub>)<sup>(1) </sup>arising from cluster algebra</em>, Naoto Okubo and Takao Suzuki, Int. Math. Res. Not. <strong>2022</strong>(9) 6561-6607 (2022).<br />
<br />
(2) <em>An affine Weyl group action on the basic hypergeometric series arising from the q-Garnier system,</em> Taiki Idomoto and Takao Suzuki, Lett. Math.Phys. <strong>112</strong>(6) (2022).<br />
<br />
(3) <em>A continuous limit of the q-Garnier system,</em> Kazuya Matsugashita and Takao Suzuki, RIMS Kokyuroku Bessatsu <strong>B96</strong> 101-116 (2024)."
["research_results"]=>
string(0) ""
["research_results_en"]=>
string(0) ""
["researchmap"]=>
string(29) "http://researchmap.jp/suzukit"
["researchoverview"]=>
string(0) ""
["academic_society"]=>
string(15) "日本数学会"
["academic_society_en"]=>
string(33) "The Mathematical Society of Japan"
["activities"]=>
string(79) "日本数学会 地方区・全国区代議員(2019年3月〜2022年2月)"
["activities_en"]=>
string(0) ""
["university"]=>
string(12) "神戸大学"
["university_en"]=>
string(15) "Kobe University"
["graduate_school"]=>
string(12) "神戸大学"
["graduate_school_en"]=>
string(15) "Kobe University"
["monograph"]=>
string(77) "Affine Weyl group symmetry of the Garnier system、神戸大学、2004年3月"
["monograph_en"]=>
string(77) "Affine Weyl group symmetry of the Garnier system, Kobe University, March 2004"
["career"]=>
string(115) "2011年 大阪府立大学教育拠点形成教員
2012年 近畿大学講師
2016年 近畿大学准教授"
["career_en"]=>
string(0) ""
["advise"]=>
string(201) "大学を卒業して社会に出た後でも勉強は常に必要となります。大学では単に知識を覚えるのではなく、新しい知識を身に付ける能力を養って下さい。"
["advise_en"]=>
string(0) ""
["recommend"]=>
string(0) ""
["recommend_en"]=>
string(0) ""
["hobby"]=>
string(0) ""
["hobby_en"]=>
string(0) ""
["awards"]=>
string(81) "全学共通教育ベストティーチャー賞(神戸大学、2010年10月)"
["awards_en"]=>
string(0) ""
["group_name"]=>
string(21) "特殊関数研究室"
["group_name_en"]=>
string(28) "Special Functions Laboratory"
["teacher_room"]=>
string(30) "31号館6階鈴木准教授室"
["teacher_room_en"]=>
string(0) ""
["extension_no"]=>
string(4) "4064"
["email"]=>
string(24) "suzuki@math.kindai.ac.jp"
["url1"]=>
string(48) "https://www.math.kindai.ac.jp/laboratory/suzuki/"
["url1_en"]=>
string(0) ""
["url2"]=>
string(0) ""
["url2_en"]=>
string(0) ""
["list_title"]=>
string(84) "関数を学ぶことによって、科学の無限の可能性を体感できる。"
["list_title_en"]=>
string(0) ""
["list_detail"]=>
string(264) "複素領域上の微分・差分方程式、およびその解として定義される特殊関数について研究しています。特殊関数は純粋数学及び応用数学の様々な分野と繫がりのある、とても魅力的な研究対象です。"
["list_detail_en"]=>
string(284) "My research field is the theory of special functions which are defined by differential or difference equations in complex domains.
These special functions are related to various fields of pure mathematics and applied mathematics.
Therefore they are very interesting research object."
["caption"]=>
string(28) "A型離散パンルヴェ系"
["caption_en"]=>
string(35) "Discrete Painlevé system of type A"
["html_keywords1"]=>
string(12) "特殊関数"
["html_keywords2"]=>
string(12) "可積分系"
["html_keywords3"]=>
string(15) "微分方程式"
["html_keywords1_en"]=>
string(17) "Special functions"
["html_keywords2_en"]=>
string(18) "Integrable systems"
["html_keywords3_en"]=>
string(22) "Differential equations"
["sci_display_flag"]=>
NULL
["metric"]=>
string(1) "0"
["laboratory"]=>
NULL
["keyword"]=>
string(103) "方程式,ベクトル・行列,線形代数,数学、解析学,関数,微分積分,複素数,組合せ"
["edited_at"]=>
string(19) "2025-02-19 14:19:38"
["created_at"]=>
string(19) "2024-04-01 00:10:25"
["updated_at"]=>
string(19) "2025-10-06 00:56:28"
["pic"]=>
string(45) "/data/sci_info/images/pic_01_suzuki_takao.jpg"
["img"]=>
string(45) "/data/sci_info/images/img_01_suzuki_takao.jpg"
}