教員・研究員紹介
-
池田 徹
(いけだ とおる)
- 教授 博士(数理科学)
-
所属学科/理学科 数学コース
所属専攻/理学専攻
3次元多様体は任意の点の周囲に3次元座標系を描ける空間です。全体の姿を見るのは難しいですが、空間や曲面を切ったり貼ったりして、対称性などの幾何的性質を研究しています。
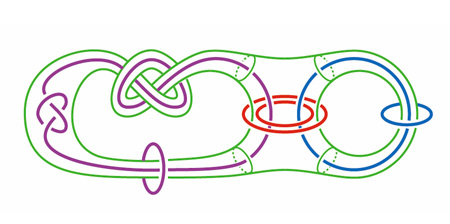
対称性を持つ絡み目の外部空間
| 専門 |
位相幾何学、3次元多様体論、結び目理論 |
| 担当科目(学部) |
数学講究(3)、数学講究(8)、集合と位相(1)、近大ゼミ1、幾何学(2) |
| 担当科目(大学院) |
多様体特論、3次元多様体特論、数理解析特別研究、多様体特殊研究 |
| 主な研究テーマ |
3次元多様体上の有限群作用の研究
結び目・空間グラフの対称性の研究 |
| 代表的な研究業績 |
(1) Realization of graph symmetries through spatial embeddings into the 3-sphere, Topol. Appl. 282 (2020), 107313.
(2) Cyclically symmetric hyperbolic spatial graphs in 3-manifolds, Geom. Dedicata 170 (2014), 177--183.
(3) Finite group actions on homologically peripheral 3-manifolds, Math. Proc. Cambridge Philos. Soc. 151 (2011), 319--337.
|
| 研究内容・研究成果 |
|
| researchmap |
http://researchmap.jp/read0057230/ |
| 所属学協会 |
日本数学会 |
| 出身大学 |
東京大学理学部数学科 |
| 出身大学院 |
東京大学大学院数理科学研究科数理科学専攻(修士課程、博士課程) |
| 論文名、取得大学、取得年月 |
Finite group actions on 3-manifolds、東京大学、2000年3月 |
| 主な経歴 |
学術振興会特別研究員(1999~2000年)、高知医科大学助教授(2000年)、高知大学助教授(2003年)、高知大学准教授(2007年)、近畿大学教授(2014年) |
| 学生へのアドバイス |
教科書や講義ノートを鵜呑みにせず、気になったところは小さなことでも自分のアタマでじっくり考える習慣をつけてほしい。 |
| 学生に薦めたい書物 |
M. ガッセン 完全なる証明 文春文庫
マリオ・リヴィオ 神は数学者か? 早川書房 |
多様体研究室
教員・研究員紹介
array(88) {
["professor_id"]=>
string(3) "640"
["site"]=>
string(3) "sci"
["html"]=>
string(13) "01_ikeda_toru"
["login_id"]=>
string(23) "ikeda@math.kindai.ac.jp"
["login_pw"]=>
string(64) "8ebcbb7bffa0f15379b31473f5b66e9e36134c77e255e9dce400f6f0b255f300"
["name"]=>
string(10) "池田 徹"
["name_en"]=>
string(10) "IKEDA Toru"
["name_kana"]=>
string(19) "いけだ とおる"
["jobtype"]=>
string(1) "1"
["degree"]=>
string(24) "博士(数理科学)"
["degree_en"]=>
string(31) "Doctor of Mathematical Sciences"
["department"]=>
string(30) "department_science_mathematics"
["department_txt"]=>
string(0) ""
["department_txt_en"]=>
string(0) ""
["major1"]=>
string(23) "graduate_school_science"
["major2"]=>
string(0) ""
["category1"]=>
string(32) "research_mathematics_and_physics"
["class1"]=>
string(34) "research_mathematics_and_physics02"
["category2"]=>
string(0) ""
["class2"]=>
NULL
["category3"]=>
string(0) ""
["class3"]=>
NULL
["specialty"]=>
string(57) "位相幾何学、3次元多様体論、結び目理論"
["specialty_en"]=>
string(35) "Topology, 3D Manifolds, Knot Theory"
["subject"]=>
string(85) "数学講究(3)、数学講究(8)、集合と位相(1)、近大ゼミ1、幾何学(2)"
["subject_en"]=>
string(0) ""
["subject_graduate"]=>
string(91) "多様体特論、3次元多様体特論、数理解析特別研究、多様体特殊研究"
["subject_graduate_en"]=>
string(0) ""
["research_theme"]=>
string(107) "3次元多様体上の有限群作用の研究
結び目・空間グラフの対称性の研究"
["research_theme_en"]=>
string(75) "Finite Group Actions on 3-Manifolds
Symmetries of Knots and Spatial Graphs"
["research_record"]=>
string(517) "(1) Realization of graph symmetries through spatial embeddings into the 3-sphere, Topol. Appl. 282 (2020), 107313.<br />
<br />
<br />
<br />
(2) Cyclically symmetric hyperbolic spatial graphs in 3-manifolds, Geom. Dedicata 170 (2014), 177--183.<br />
<br />
<br />
<br />
(3) Finite group actions on homologically peripheral 3-manifolds, Math. Proc. Cambridge Philos. Soc. 151 (2011), 319--337.<br />
<br />
<br />
<br />
"
["research_record_en"]=>
string(451) "(1) Realization of graph symmetries through spatial embeddings into the 3-sphere, Topol. Appl. 282 (2020), 107313.<br />
<br />
<br />
<br />
(2) Cyclically symmetric hyperbolic spatial graphs in 3-manifolds, Geom. Dedicata 170 (2014), 177--183.<br />
<br />
<br />
<br />
(3) Finite group actions on homologically peripheral 3-manifolds, Math. Proc. Cambridge Philos. Soc. 151 (2011), 319--337."
["research_results"]=>
string(0) ""
["research_results_en"]=>
string(0) ""
["researchmap"]=>
string(34) "http://researchmap.jp/read0057230/"
["researchoverview"]=>
string(0) ""
["academic_society"]=>
string(15) "日本数学会"
["academic_society_en"]=>
string(0) ""
["activities"]=>
string(0) ""
["activities_en"]=>
string(0) ""
["university"]=>
string(30) "東京大学理学部数学科"
["university_en"]=>
string(27) "BE from University of Tokyo"
["graduate_school"]=>
string(93) "東京大学大学院数理科学研究科数理科学専攻(修士課程、博士課程)"
["graduate_school_en"]=>
string(34) "ME and DE from University of Tokyo"
["monograph"]=>
string(64) "Finite group actions on 3-manifolds、東京大学、2000年3月"
["monograph_en"]=>
string(0) ""
["career"]=>
string(201) "学術振興会特別研究員(1999~2000年)、高知医科大学助教授(2000年)、高知大学助教授(2003年)、高知大学准教授(2007年)、近畿大学教授(2014年)"
["career_en"]=>
string(0) ""
["advise"]=>
string(171) "教科書や講義ノートを鵜呑みにせず、気になったところは小さなことでも自分のアタマでじっくり考える習慣をつけてほしい。"
["advise_en"]=>
string(0) ""
["recommend"]=>
string(117) "M. ガッセン 完全なる証明 文春文庫
マリオ・リヴィオ 神は数学者か? 早川書房"
["recommend_en"]=>
string(0) ""
["hobby"]=>
string(0) ""
["hobby_en"]=>
string(0) ""
["awards"]=>
string(0) ""
["awards_en"]=>
string(0) ""
["group_name"]=>
string(18) "多様体研究室"
["group_name_en"]=>
string(19) "Manifold Laboratory"
["teacher_room"]=>
string(27) "31号館4階池田教授室"
["teacher_room_en"]=>
string(0) ""
["extension_no"]=>
string(4) "4065"
["email"]=>
string(23) "ikeda@math.kindai.ac.jp"
["url1"]=>
string(47) "https://www.math.kindai.ac.jp/laboratory/ikeda/"
["url1_en"]=>
string(0) ""
["url2"]=>
string(0) ""
["url2_en"]=>
string(0) ""
["list_title"]=>
string(73) "3次元トポロジーを用いて様々な空間図形を探究する。"
["list_title_en"]=>
string(0) ""
["list_detail"]=>
string(245) "3次元多様体は任意の点の周囲に3次元座標系を描ける空間です。全体の姿を見るのは難しいですが、空間や曲面を切ったり貼ったりして、対称性などの幾何的性質を研究しています。"
["list_detail_en"]=>
string(268) "A 3-manifold is a space in which a 3D coordinate system can be drawn around arbitrary points. Although it’s difficult to visualize an entire 3-manifold, work here involves cutting and pasting spaces and curves in order to study geometric properties such as symmetry."
["caption"]=>
string(42) "対称性を持つ絡み目の外部空間"
["caption_en"]=>
string(23) "Symmetric link exterior"
["html_keywords1"]=>
string(15) "位相幾何学"
["html_keywords2"]=>
string(19) "3次元多様体論"
["html_keywords3"]=>
string(15) "結び目理論"
["html_keywords1_en"]=>
string(8) "Topology"
["html_keywords2_en"]=>
string(19) "3-manifold topology"
["html_keywords3_en"]=>
string(11) "Knot theory"
["sci_display_flag"]=>
NULL
["metric"]=>
string(1) "0"
["laboratory"]=>
NULL
["keyword"]=>
string(41) "図形,トポロジー,数学、幾何学"
["edited_at"]=>
string(19) "2025-09-29 11:27:08"
["created_at"]=>
string(19) "2024-04-01 00:10:25"
["updated_at"]=>
string(19) "2025-10-06 00:56:28"
["pic"]=>
string(43) "/data/sci_info/images/pic_01_ikeda_toru.jpg"
["img"]=>
string(43) "/data/sci_info/images/img_01_ikeda_toru.jpg"
["pdf"]=>
string(40) "/data/sci_info/pdf/pdf_01_ikeda_toru.pdf"
}

