-
- 研究所
高速遊泳する「近大マグロ」の尾びれを教材に活用 近大ならではのSDGsな実習で、理工学部生が生体エネルギーを学ぶ
2024.04.09
-
近畿大学理工学部で「バッテリー人材育成プログラム」を開講 脱炭素社会の実現に寄与する次世代のエネルギー人材を育成
2024.03.28
-
試薬等に用いられるホタルルシフェリンの画期的な合成方法を開発 今後より安価で迅速な製造工程の確立に期待
2024.03.13
-
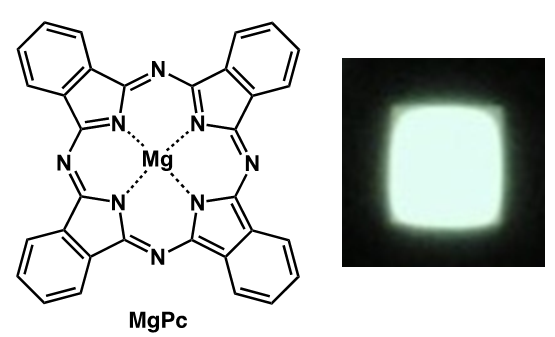
磁場誘起型有機円偏光発光ダイオードの円偏光発生メカニズムを解明 円偏光発光ダイオードの高性能化の設計指針を提示
2024.02.26
-
ペロブスカイト量子ドットからマルチカラー円偏光の発生に成功 3D表示用有機ELディスプレイ等の製造コスト削減に期待
2024.01.19